 La meccanica della frattura, ovvero perchè gli oggetti si rompono quando ne hanno voglia loro e
non quando avrei immaginato io
La meccanica della frattura, ovvero perchè gli oggetti si rompono quando ne hanno voglia loro e
non quando avrei immaginato io
 La meccanica della frattura, ovvero perchè gli oggetti si rompono quando ne hanno voglia loro e
non quando avrei immaginato io
La meccanica della frattura, ovvero perchè gli oggetti si rompono quando ne hanno voglia loro e
non quando avrei immaginato io
Delle possibili modalità di collasso di una struttura, la frattura è quella che interessa precipuamente le bocche da fuoco. Ergo il moderno fochino scientifico non può ignorare alcuni principi fondamentali di quella branca della scienza delle costruzioni detta meccanica della frattura. Cercheremo qui nel seguito di spiegare intuitivamente ai profani della materia cosa sia questa sistematizzazione matematica di alcuni fenomeni fisici, e perché sia così importante nell'ambito pirotecnico.


 prima linea ferroviaria defininbile
compiutamente tale, circa nove miglia inglesi (pressappoco quindici
chilometri) percorse in poco più di un'ora da Stockton a Darlington in quel della perfida
Albione. Nel giro di pochi decenni la strada ferrata divenne IL trasporto
terrestre di massa. Rapidamente furono concepite ed apportate migliorie
all'armamanto, alla
trazione a
vapore, al materiale rotabile ed alla tecnica della circolazione. Nel
frattempo l'ingegneria civile concepiva opere fino a poco
prima nemmeno immaginabili dalla più fervida immaginazione, capostipite delle quali fu la pionieristica
strada ferrata da Genova Piazza Principe a Torino
Porta Nuova via traforo dei Giovi, tremilacinquecento metri finiti di scavare
nel 1853 con mazzagubbia e polvere nera in condizioni geologiche proibitive
ben prima che Germano Sommelier introducesse, presso gli scavi per
il traforo del Frejus, la perforatrice meccanica ad aria
compressa.
Il raggiungimento di velocità
"innaturali" da parte dei rotabili pose
all'attenzione degli ingegneri ottocenteschi un fenomeno nuovo, decisamente
sgradito ed alla prima apparenza inspiegabile. Trattavasi dell'improvvisa
rottura di schianto delle sale montate (il complesso di assile, ruote e boccole)
dei rotabili, molto spesso in corispondenza dell'attacco del fusello
(la sezione compresa fra la faccia esterna della ruota e la faccia interna della
boccola). A questo fenomeno venne dato il nome di "fatica". <<Le prime
prima linea ferroviaria defininbile
compiutamente tale, circa nove miglia inglesi (pressappoco quindici
chilometri) percorse in poco più di un'ora da Stockton a Darlington in quel della perfida
Albione. Nel giro di pochi decenni la strada ferrata divenne IL trasporto
terrestre di massa. Rapidamente furono concepite ed apportate migliorie
all'armamanto, alla
trazione a
vapore, al materiale rotabile ed alla tecnica della circolazione. Nel
frattempo l'ingegneria civile concepiva opere fino a poco
prima nemmeno immaginabili dalla più fervida immaginazione, capostipite delle quali fu la pionieristica
strada ferrata da Genova Piazza Principe a Torino
Porta Nuova via traforo dei Giovi, tremilacinquecento metri finiti di scavare
nel 1853 con mazzagubbia e polvere nera in condizioni geologiche proibitive
ben prima che Germano Sommelier introducesse, presso gli scavi per
il traforo del Frejus, la perforatrice meccanica ad aria
compressa.
Il raggiungimento di velocità
"innaturali" da parte dei rotabili pose
all'attenzione degli ingegneri ottocenteschi un fenomeno nuovo, decisamente
sgradito ed alla prima apparenza inspiegabile. Trattavasi dell'improvvisa
rottura di schianto delle sale montate (il complesso di assile, ruote e boccole)
dei rotabili, molto spesso in corispondenza dell'attacco del fusello
(la sezione compresa fra la faccia esterna della ruota e la faccia interna della
boccola). A questo fenomeno venne dato il nome di "fatica". <<Le prime  ricerche sistematiche sui fenomeni di fatica furono quelle di Wöhler [a
destra nella foto, n.d.r.], il quale intorno al 1850 iniziò una lunga serie di
studi protrattisi poi per circa venti anni, pervenendo a risultati di notevole
interesse. Non riuscendo a spiegare il gran numero di rotture improvvise di
assali di vagoni ferroviari,
ricerche sistematiche sui fenomeni di fatica furono quelle di Wöhler [a
destra nella foto, n.d.r.], il quale intorno al 1850 iniziò una lunga serie di
studi protrattisi poi per circa venti anni, pervenendo a risultati di notevole
interesse. Non riuscendo a spiegare il gran numero di rotture improvvise di
assali di vagoni ferroviari, 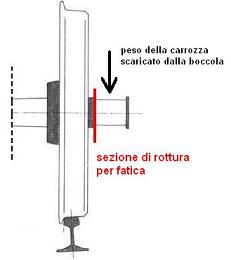 avvenute sotto carichi di esercizio e senza
apprezzabili deformazioni [a sinistra nello schema, n.d.r.], egli eseguì una serie di
esperienze su provini in acciaio soggetti a sollecitazioni cicliche ad ampiezza
costante e rappresentò i risultati in diagrammi nei quali, in funzione dei
parametri di sollecitazione della prova, riportò la vita a fatica N, cioè il
numero di cicli che provocavano la rottura del provino>> (1). I
risultati raggiunti furono pubblicati dallo stesso Wöhler nel 1871 (2)(3).
Per la prima volta si impose all'attenzione degli scienziati un
comportamento dei materiali difforme dalla teoria dell'elasticità
precedentemente sviluppata da Navier, Eulero, Bernoulli, Hooke e seguaci.
Per la prima volta ci si rendeva conto che in determinate condizioni,
anche sotto sollecitazioni basse, non vi è proporzionalità fra cause
ed effetti strutturali. Tuttavia gli studi compiuti non approfondirono ancora
gli aspetti teorici ed analitici della questione: <<gli studi sui
fenomeni di fatica continuarono ad essere, per oltre un secolo, a carattere
sperimentale e non aggiunsero quasi nulla di concettuale al lavoro di Wöhler. Un
notevole progresso è stato compiuto, attorno al 1960, mediante un approccio
analitico: tale approccio è basato sulla meccanica della frattura>>
(1).
avvenute sotto carichi di esercizio e senza
apprezzabili deformazioni [a sinistra nello schema, n.d.r.], egli eseguì una serie di
esperienze su provini in acciaio soggetti a sollecitazioni cicliche ad ampiezza
costante e rappresentò i risultati in diagrammi nei quali, in funzione dei
parametri di sollecitazione della prova, riportò la vita a fatica N, cioè il
numero di cicli che provocavano la rottura del provino>> (1). I
risultati raggiunti furono pubblicati dallo stesso Wöhler nel 1871 (2)(3).
Per la prima volta si impose all'attenzione degli scienziati un
comportamento dei materiali difforme dalla teoria dell'elasticità
precedentemente sviluppata da Navier, Eulero, Bernoulli, Hooke e seguaci.
Per la prima volta ci si rendeva conto che in determinate condizioni,
anche sotto sollecitazioni basse, non vi è proporzionalità fra cause
ed effetti strutturali. Tuttavia gli studi compiuti non approfondirono ancora
gli aspetti teorici ed analitici della questione: <<gli studi sui
fenomeni di fatica continuarono ad essere, per oltre un secolo, a carattere
sperimentale e non aggiunsero quasi nulla di concettuale al lavoro di Wöhler. Un
notevole progresso è stato compiuto, attorno al 1960, mediante un approccio
analitico: tale approccio è basato sulla meccanica della frattura>>
(1). La risposta la diede per la prima volta l'ingegnere Alan
Arnold Griffith (a sinistra) nel
1920 (4), che formulò la prima teoria energetica
della frattura fragile adducendo il concetto di energia di
deformazione elastica e di energia di formazione di superficie libera. In
sintesi: un corpo elastico caricato da forze esterne si deforma. Tale
deformazione si accompagna ad uno stato di sforzo all'interno del materiale. Il
corpo è quindi sede di accumulo di energia potenziale di deformazione elastica
(sforzo per deformazione = energia per
unità di volume). Sia adesso il corpo criccato da una fessura deliberata
o da un (inevitabile) difetto seppur invisibile ad occhio nudo. Se questa
fessura dovesse propagarsi verrebbe a crearsi una nuova porzione di
superficie libera (le due facce della frattura propagata). Per creare nuova superficie
libera è necessario compiere un lavoro per spezzare i legami nel
materiale ovvero spendere energia, in una quantità pari al prodotto fra l'area
della nuova superficie libera per l'energia G necessaria per la creazione di una
unità di superficie
libera (il valore di cui è una proprietà intrinseca del materiale). Quando la frattura si propaga i suoi
dintorni si "scaricano" (gli sforzi diminuiscono) e l'energia
di deformazione precedentemente accumulata nel
corpo si perde. Griffith constatò questo: se la frattura propagandosi
richiede un'energia di formazione minore di quella che il corpo può cedere a causa della
propagazione, ovvero a causa dello "scaricamento" dello stato di sforzo
e deformazione nei pressi della frattura, allora la frattura si propaga spontaneamente.
Ovvero quando il corpo, durante la propagazione
di una frattura, è in grado di rilasciare (a causa dello scarico di
alcune sue parti) energia (precedentemente immagazinata quale
energia potenziale di deformazione elastica) a sufficienza per propagare
la detta frattura (ovvero in quantità superiore a quella necessaria a
creare nuova superficie di frattura), allora la frattura si propaga e si
ha generalmente la rottura di schianto
. Per Griffith il problema si
inquadrava sostanzialmente così: un corpo preferisce stare ad un
livello energetico stabile e se non ci si trova fa di tutto per
raggiungerlo spontaneamente. Forse la teoria di Griffith era troppo innovativa
per i tempi. Sta di fatto che, nonostante l'importanza capitale
dell'argomento, i suoi studi non ebbero diffusione di massa, e la teoria energetica della
frattura fragile rimase una curiosità accademica per pochi esperti.
La risposta la diede per la prima volta l'ingegnere Alan
Arnold Griffith (a sinistra) nel
1920 (4), che formulò la prima teoria energetica
della frattura fragile adducendo il concetto di energia di
deformazione elastica e di energia di formazione di superficie libera. In
sintesi: un corpo elastico caricato da forze esterne si deforma. Tale
deformazione si accompagna ad uno stato di sforzo all'interno del materiale. Il
corpo è quindi sede di accumulo di energia potenziale di deformazione elastica
(sforzo per deformazione = energia per
unità di volume). Sia adesso il corpo criccato da una fessura deliberata
o da un (inevitabile) difetto seppur invisibile ad occhio nudo. Se questa
fessura dovesse propagarsi verrebbe a crearsi una nuova porzione di
superficie libera (le due facce della frattura propagata). Per creare nuova superficie
libera è necessario compiere un lavoro per spezzare i legami nel
materiale ovvero spendere energia, in una quantità pari al prodotto fra l'area
della nuova superficie libera per l'energia G necessaria per la creazione di una
unità di superficie
libera (il valore di cui è una proprietà intrinseca del materiale). Quando la frattura si propaga i suoi
dintorni si "scaricano" (gli sforzi diminuiscono) e l'energia
di deformazione precedentemente accumulata nel
corpo si perde. Griffith constatò questo: se la frattura propagandosi
richiede un'energia di formazione minore di quella che il corpo può cedere a causa della
propagazione, ovvero a causa dello "scaricamento" dello stato di sforzo
e deformazione nei pressi della frattura, allora la frattura si propaga spontaneamente.
Ovvero quando il corpo, durante la propagazione
di una frattura, è in grado di rilasciare (a causa dello scarico di
alcune sue parti) energia (precedentemente immagazinata quale
energia potenziale di deformazione elastica) a sufficienza per propagare
la detta frattura (ovvero in quantità superiore a quella necessaria a
creare nuova superficie di frattura), allora la frattura si propaga e si
ha generalmente la rottura di schianto
. Per Griffith il problema si
inquadrava sostanzialmente così: un corpo preferisce stare ad un
livello energetico stabile e se non ci si trova fa di tutto per
raggiungerlo spontaneamente. Forse la teoria di Griffith era troppo innovativa
per i tempi. Sta di fatto che, nonostante l'importanza capitale
dell'argomento, i suoi studi non ebbero diffusione di massa, e la teoria energetica della
frattura fragile rimase una curiosità accademica per pochi esperti.
 Altro modo di inquadrare il
medesimo problema è l'approccio tensionale, che fu
proposto compiutamente per la prima volta da George Rankine Irwin (a sinistra) negli anni Cinquanta (5):
<<l'evento decisivo per lo
sviluppo di questa nuova disciplina si verificò [...] durante la Seconda Guerra
Mondiale, quando vi furono i famosi cedimenti delle navi americane "Liberty",
che erano state costruite secondo un progetto innovativo con lo scafo
Altro modo di inquadrare il
medesimo problema è l'approccio tensionale, che fu
proposto compiutamente per la prima volta da George Rankine Irwin (a sinistra) negli anni Cinquanta (5):
<<l'evento decisivo per lo
sviluppo di questa nuova disciplina si verificò [...] durante la Seconda Guerra
Mondiale, quando vi furono i famosi cedimenti delle navi americane "Liberty",
che erano state costruite secondo un progetto innovativo con lo scafo  completamente saldato e non chiodato, in modo da
risparmiare sui tempi di realizzazione delle navi. Delle 2700 navi che erano
state costruite circa 400 presentarono cedimenti, di cui almeno 90 gravi e 20
catastrofici [n.d.c.: a destra uno di questi "incidenti" in una foto tratta da
statisticalengineering.com
], con la rottura completa della nave in due parti. Le ricerche condotte
su questi cedimenti mostrarono che non erano stati commessi errori di progetto
in quanto gli sforzi erano sempre inferiori a quelli ammissibili dei materiali,
però si constatò che le fratture iniziavano sempre dalle saldature, quando
vi erano difetti, oppure da intagli in zone di forti concentrazioni degli sforzi
e che il materiale sottoposto alla prova di Charpy (7) rivelava bassi valori
di tenacità. Venne istituito un gruppo di ricerca sotto la guida di Irwin nel
Naval Research Laboratory, che diede un decisivo impulso allo sviluppo della
meccanica della frattura>> (6). Irwin osservò lo stato tensionale nei
pressi dell'apice della frattura. Studiando il
problema elastico di una lastra tesa con un incavo sul contorno
(problema fra l'altro già affrontato in precedenza da altri autori fra cui Westergaard,
Muskhelishvili, Williams ed i pionieristici Kirsch e Inglis), giunse a concludere che,
in sezione trasversale, avvicinandosi al culmine dell'incavo lo stato tensionale
aumenta tanto più quanto più è acuminato l'incavo. Al limite per fessure
idealmente acuminate lo stato di sforzo tende ad infinito al tendere a zero
della distanza dall'apice della fessura. In questo caso non è che il corpo ceda
automaticamente, in quanto la divergenza degli sforzi avviene per un'estensione
infinitesima di spazio attorno al culmine (tipico caso in cui si ha a che fare
con un qualcosa tipo il prodotto zero per infinito).
completamente saldato e non chiodato, in modo da
risparmiare sui tempi di realizzazione delle navi. Delle 2700 navi che erano
state costruite circa 400 presentarono cedimenti, di cui almeno 90 gravi e 20
catastrofici [n.d.c.: a destra uno di questi "incidenti" in una foto tratta da
statisticalengineering.com
], con la rottura completa della nave in due parti. Le ricerche condotte
su questi cedimenti mostrarono che non erano stati commessi errori di progetto
in quanto gli sforzi erano sempre inferiori a quelli ammissibili dei materiali,
però si constatò che le fratture iniziavano sempre dalle saldature, quando
vi erano difetti, oppure da intagli in zone di forti concentrazioni degli sforzi
e che il materiale sottoposto alla prova di Charpy (7) rivelava bassi valori
di tenacità. Venne istituito un gruppo di ricerca sotto la guida di Irwin nel
Naval Research Laboratory, che diede un decisivo impulso allo sviluppo della
meccanica della frattura>> (6). Irwin osservò lo stato tensionale nei
pressi dell'apice della frattura. Studiando il
problema elastico di una lastra tesa con un incavo sul contorno
(problema fra l'altro già affrontato in precedenza da altri autori fra cui Westergaard,
Muskhelishvili, Williams ed i pionieristici Kirsch e Inglis), giunse a concludere che,
in sezione trasversale, avvicinandosi al culmine dell'incavo lo stato tensionale
aumenta tanto più quanto più è acuminato l'incavo. Al limite per fessure
idealmente acuminate lo stato di sforzo tende ad infinito al tendere a zero
della distanza dall'apice della fessura. In questo caso non è che il corpo ceda
automaticamente, in quanto la divergenza degli sforzi avviene per un'estensione
infinitesima di spazio attorno al culmine (tipico caso in cui si ha a che fare
con un qualcosa tipo il prodotto zero per infinito).
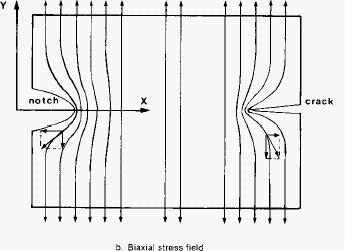
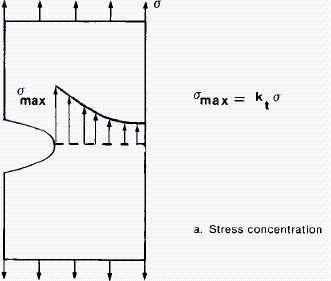
A sinistra: il disturbo indotto da un incavo ("notch") ed una fessura ("crack") sulle linee isostatiche che seguono la direzione dello sforzo principale di trazione in un provino teso. A destra la crescita di intensità dello stato di sforzo all'avvicinarsi al culmine del difetto (figure da hghouston.com).

Una delle più illustri vittime della nuova branca della meccanica: il "de Havilland Comet" DH-106 (nella foto tratta da marville.org un Comet in servizio per l'Aeronautica militare canadese) fu il primo aviogetto commerciale prodotto dall'industria aeronautica. Considerato un gioiello dell'ingegneria britannica, prese il volo per la prima volta nel 1949. Nel giro di cinque anni si era già procurato una fama a dir poco sinistra, a causa di alcuni incidenti catastrofoci che flagellarono gli esemplari fin dalla prima serie. Il primo avvenne all'aeroporto di Ciampino, allora massimo scalo italiano, il 26 ottobre 1952: il Comet G-ALYZ della compagnia inglese BOAC precipitò in fase di decollo. Meno di due anni dopo, il 10 gennaio 1954 il suo gemello G-ALYP, della medesima compagnia, partì da Ciampino per inabissarsi al largo dell'Elba. Di 114 esemplari prodotti e suddivisi in sei serie, tredici non arrivarono a destinazione. Per cinque di essi fu accertato inequivocabilmente il problema strutturale. Un solo incidente fatale fu attribuito senz'ombra di dubbio a fattori diversi (in ispecie fu constatato un errore umano). Gli altri casi rimasero nel dubbio. La commissione di inchiesta che si occupò dei primi incidenti attribuì i collassi strutturali alla propagazione di cricche (in particolare dagli spigoli vivi e dalle saldature) per eccessiva fatica, provocata dalla inopportuna collocazione dei quattro motori a turbogetto all'interno del corpo delle ali che, ancorchè aerodinamicamente ed esteticamente pregevole, sottoponeva l'intera struttura a vibrazioni intensissime. Si riscontrò che le cricche si propagavano sino a raggiungere un'estensione tale da indurre un'intensificazione degli sforzi incompatibile con le caratteristiche di resistenza del materiale strutturale adottato. In particolare furono additati quali punti di nucleazione (di origine) del fenomeno gli oblò, che negli apparecchi della prima serie erano costituiti da finestrini rettangolari a spigoli vivi, sfortunata scelta di geometria, in seguito definitivamente abbandonata a favore delle forme attuali arrotondate.

Altra vittima notevole della meccanica della frattura: pare che il celeberrimo piroscafo Titanic fosse stato costruito tirando al risparmio con acciaio ordinario (nel senso spregiativo del termine) la cui qualità risultava poco idonea alle applicazioni strutturali navali e che risultò oltremodo infragilito dal clima lungo la rotta nordatlantica, determinando la propagazione incontrollata dello squarcio che portò la nave al disastro. E' oggetto di discussione fra gli appassionati la possibilità che la nave avrebbe potuto sopravvivere all'incidente nel caso in cui fosse stato adottato per il fasciame e le ordinate un acciaio più tenace, poco sensibile alle temperature gelide delle acque subpolari.
Si distinguono tre modalità di frattura a seconda del cinematismo con cui questa avviene (modo I o trazione nel piano, modo II o taglio nel piano e modo III o taglio fuori piano o lacerazione, da physicsarchives.com ):
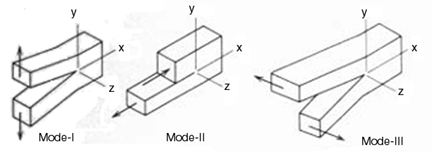
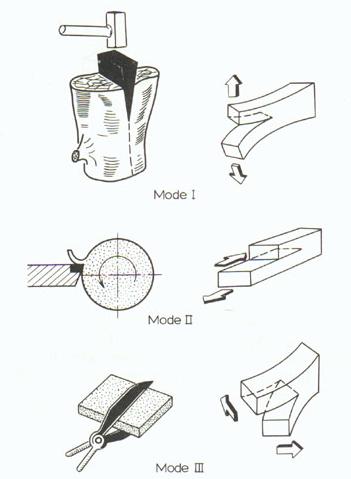
Guardando ad esempio il modo primo, quello a trazione nel piano della lastra, la soluzione nell'approccio di Irwin è riportata nelle formulacce di seguito, dove viene quantificato il valore delle componenti del tensore di sforzo in funzione di r, la distanza dall'apice della fessura, e tetha, l'angolo di elevazione del raggio vettore rispetto al piano che contiene la fessura. Gli sforzi sono ovunque proporzionali ad un fattore K detto fattore di intensificazione degli sforzi, il quale dipende altresì dal modo di propagazione della frattura e quindi spesso viene indicato con Ki dove i può valere I,II o III (si usano tradizionalmente i numeri romani). Il criterio di propagazione della frattura secondo Irwin è il seguente: fintantoché Ki è minore di un valore critico Kic, caratteristica del materiale, la frattura non si propaga. Allorquando Ki eguaglia o supera Kic la frattura si propaga di schianto secondo il modo i-esimo. Ki dipende secondo legge affatto lineare dalla geometria e dalle dimensioni del problema e dall'intensità del carico applicato. Il calcolo dei fattori K può essere svolto con carta e penna solamente nel caso di geometrie elementari per le quali esistono soluzioni analitiche note. Nei casi più generali la valutazione è demandata al calcolatore programmato per la risoluzione numerica mediante il metodo degli elementi finiti.
|
|
|
|
A sinistra: la soluzione di Irwin in termini di componenti del tensore di sforzo per il modo primo; al centro il significato dei termini del tensore di sforzo (da sv.vt.edu). Si noti, nelle formule che esprimono le componenti costituenti il tensore di sforzo, la divergenza secondo la radice quadrata della distanza all'approssimarsi all'apice della fessura. A destra: la visualizzazione grafica dei risultati di una valutazione tensionale mediante il metodo degli elementi finiti.
Gli approcci energetici e tensionali sono equivalenti ed esistono relazioni analitiche fra l'energia superficiale di formazione di frattura ed i fattori critici di intensificazione degli sforzi. Successivamente sono poi stati proposti e validati notevoli sviluppi dei fondamentali concetti, per i materiali e le situazioni più disparate (meccanica della frattura duttile, quasi-fragile o coesiva, ecc.).
Il risultato di tutti questi studi è in estrema sintesi questo: avendo a che fare con strutture criccate (p.e. saldature mal riuscite a causa di inclusioni di scorie), danneggiate o deliberatamente intagliate (pezzi meccanici quali ingranaggi, alberi a gomiti, qualunque membratura con spigoli vivi o debolmente arrotondati e rientranti, e in realtà a voler essere proprio pignoli qualunque manufatto umano, in cui una certa difettosità, seppur al di sotto di tolleranze magari strettissime, è sempre presente ancorchè impercettibile ai sensi umani), il collasso può avvenire non solo perché il materiale esaurisce la sua resistenza caratteristica, ma anche per frattura. Il collasso per frattura dipende sia dalla natura del materiale sia dalla geometria del problema sia dalla storia di carico e segue leggi di scala diverse dalla semplice proporzionalità diretta fra dimensioni e capacità portante. Oggetti uguali ma che presentano piccole differenze sotto forma di difetti, magari impercettibili ad occhio nudo, possono avere limiti e tipologie di collasso differenti. Ebbene, non avendo intenzione di addentrarci nei reconditi meandri della meccanica avanzata delle strutture (argomento che lasciamo ben volentieri alle elucubrazioni degli ingegneri civili, aeronautici e meccanici), cosa c'entra tutto ciò con i mascoli?
Il mascolo, analogamente a tutte le bocche da fuoco per le quali valgono analoghe considerazioni (dal tubo di lancio dei fuochi pirotecnici ai cannoni di Navarone), è un tubo "spesso" (così detto in gergo ingegneristico in quanto lo spessore delle pareti è notevole rispetto al diametro del foro, e viene messo in conto nelle analisi strutturali) soggetto ad una forte pressione interna. Fintantoché il mascolo si mantiene privo di difetti la sua capacità portante è data dalla resistenza allo snervamento della parete del tubo. Di fronte a questa evenienza l'ordinario mascolo (ed anche il cannoncino ed il cannone, ma a conti fatti anche il tubo Innocenti) si rivela essere enormemente sovradimensionato. Imprecisioni costruttive, corrosione e accidenti meccanici (urti, sfregamenti, caricamento...) possono generare difetti nelle pareti della canna o della base, sotto forma di fessure, incavi, camöe, intagli, bombature... Ognuno di questi difetti genera intensificazione degli sforzi, ed inoltre è sede preferenziale di corrosione che a sua volta aumenta ulteriormente l'intensificazione aggravando il difetto secondo uno sfavorevole circolo vizioso. Fintantoché l'intensificazione degli sforzi dovuti allo sparo è tale da non superare una determinata soglia il mascolo continua a comportarsi all'incirca come un corpo elastoplastico la cui capacità portante è legata allo snervamento del materiale. Allorquando dovesse verificarsi un'intensificazione critica degli sforzi, si produrrebbe la propagazione di frattura a partire dal difetto in cui l'intensificazione ha violato la soglia. A volte la frattura si propaga fino ad un'estensione corrispondente ad una stabilizzazione determinata da una favorevole redistribuzione degli sforzi; altre volte la propagazione si manifesta fino alla rottura per cedimento di schianto del pezzo. Per contenere tale pericolo è quindi possibile procedere per due vie: diminuire l'intensificazione degli sforzi, controllando che le irregolarità si mantengano entro geometrie e dimensioni di sicurezza, o aumentare le soglie critiche di innesco della frattura, usando materiali più tenaci (che hanno energia di Griffith e Kic di Irwin più alti). Alla luce di ciò si comprende il fondamento scientifico dell'abbandono dei mascoli di ghisa (la foto soprastante li mostra tristemente accantonati, dopo più di un secolo di onorato servizio pirotecnico, in attesa di miglior destino come simpatici soprammobili e portapenne); tali mascoli presentano infatti entrambe le problematiche: le superfici, già abbastanza scabre in origine per via del materiale usato e della realizzazione in grande serie non proprio certosina, sono maggiormente intaccabili da difetti, ed inoltre la tenacità del materiale è notevolmente più bassa rispetto agli acciai.
Per una trattazione più consapevole del problema si rimanda a testi specifici quali "Meccanica dei materiali" di Laura Vergani, edizioni McGraw Hill (Milano), e "Meccanica dei materiali e della frattura" di Alberto Carpinteri, edizioni Pitagora (Bologna). Presso i siti internet dei dipartimenti di ingegneria civile, meccanica e strutturale delle università italiane è possibile reperire inoltre validissime dispense in formato pdf.
(1) A. Carpinteri, in bibliografia .
(2) A. Wöhler, "Tests to determine the forces acting on railway carriage axles and the capacity of resistance of the axles", Engineering, vol. 11, 199, 1871.
(3) Per inciso, il fenomeno studiato e compreso dal buon Wöhler è esattamente quello che è accaduto ad un carro cisterna per GPL a Viareggio nell'estate del 2009. Centoquaranta anni di studio e ricerca ignorati a cuor leggero?
(4) A.A. Griffith, "The phenomena of rupture and flow in solids ", Transactions of the Royal Society of London , vol. 221, 1920.
(5) G.R. Irwin, "Analysis of stresses and strains near the end of a crack transversing a plate", Journal of applied mechanics, vol. 24, pp. 361-364, 1957.
(6) L. Vergani, in bibliografia .
(7) La prova di resilienza, o del pendolo di Augustin Georges Albert Charpy, consiste nel sottoporre all'urto di una massa battente un provino preventivamente intagliato del materiale in esame. Fornisce un parametro detto modulo di resilienza correlato alla tenacità del materiale. Effettuando la prova in camera climatica a condizioni differenti si hanno preziose informazioni sull'infragilimento dei materiali a basse temperature. La prova è attualmente standardizzata secondo la norma UNI EN 10045.